Research Investigação

A more detailed explanation

Dipolar Hard Sphere Fluid

We consider particles with dipolar interactions and predict, combining theory and numerical experi­ments (Monte Carlo simulations), phase transitions and structural changes. This is important for the development of new materials, in particular magnetic colloids, where dipolar interactions play a crucial role.

The dipolar interaction is anisotropic: it depends not only on the relative orientation of the dipoles but also on the direction of the interdipolar vector. A model of spherical hard-core particles with embedded dipoles is known as the dipolar hard-sphere fluid [1].

The dipolar potential favours the head to tail alignment of the dipoles (the configuration with the lowest energy). It can be shown that, as a consequence, the linear clusters with lowest energy are rings. Chains and rings have the same energy in the limit of very large clusters.

When the thermal energy (kinetic energy) is much larger than the dipolar energy (potential energy), the DHS model behaves as an ideal gas and no trace of chain or ring structures is found. The system is in a regime where entropy dominates. By contrast, when the temperature is low, i.e. when the dipolar energy is much larger than the kinetic energy, one expects the particles to form one or a few rings and/or chains. The DHS fluid is then in a regime where energy dominates.

In the regime studied by us the thermal and dipolar energies are similar. Therefore, one expects to find both order (clusters) and disorder (several clusters and/or isolated particles).

Simulations of DHSs were carried out for a fixed number of particles per unit volume (ρ* – the number density) and a fixed ratio, μ*², between the dipolar energy and the thermal energy (μ*² = μ²/(s 3 kBT)). Technically, the simulations were carried out in the canonical ensemble (or NVT).

In the following figure, we represent several configurations (snapshots of the system in equilibrium) obtained for various sets of ρ* and μ* and for N=5776 in 2-dimensions [2].

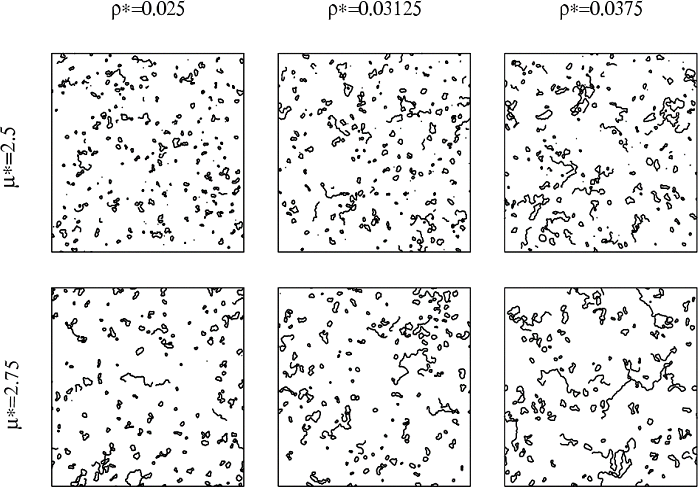
The simulations exhibit a strong tendency to form clusters of different topologies: rings, chains and several types of branched clusters. In the next figure we represent these clusters for a specific configuration of a 2-dimensional DHS:

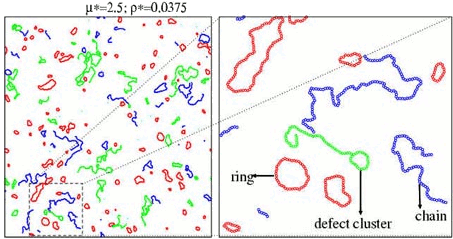
We found that, for chains, rings and defect clusters, the radius of gyration is a power of the number of particles. The measured exponent is close to 0.75, meaning that the clusters are fractals (the fractal dimension is 1/0.75) with conformational properties analogous to a 2-dimensional self avoiding random walk.

The length distributions for chains (blue) and rings (red), i.e., the mean number of clusters of each size and type for two simulations are shown in the next figure.

The system is polydisperse with well defined length (or mass) distributions that depend only on the total density and the interactions.

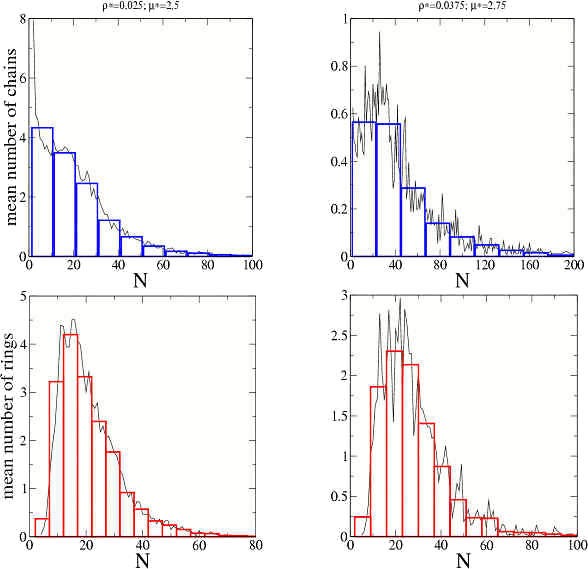
By following individual clusters we found that the clusters form, break and recombine in several ways. That is, the equilibrium state is not described by “static” clusters but by clusters that exchange particles among them. We have also shown that the the interaction between clusters is less than 1% of the total internal energy of the system.

These results led us to the hypothesis that the DHS is an IDEAL SELF ASSEMBLING SYSTEM, i.e., a system that exhibits spontaneous aggregation of the particles in non-interacting clusters, at chemical equilibrium.

Within this framework, the distribution of clusters of type k is proportional to the partition function of the clusters. We can approximate the partition function of rings and chains by using the knowledge of their conformational properties and internal energy (both suggested by the simulation results). It is then possible to define modified distributions of chains and rings that are universal, in the sense that they depend only on the (universal) exponents a and g of polymer theory (see more details here). In the next figure we show these distributions obtained from simulations and the theoretical prediction for d = 2 ( a = 0.5 and g = 1.33).

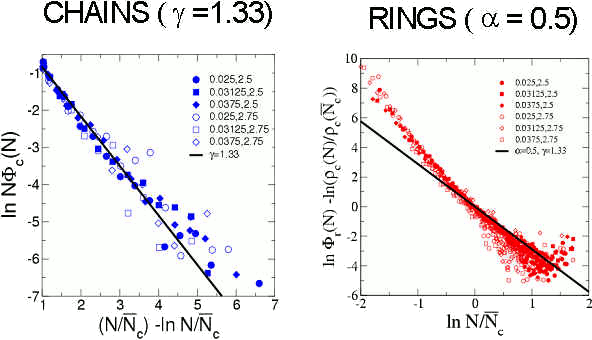
The good agreement between the simulation data and the theoretical predictions shows that the complex structure of the DHS can be described as self-assembly of ideal clusters. Under these conditions the DHS is analogous to equilibrium polymers, simpler systems where monomer aggregate into chains and rings at chemical equilibrium.

The major open question, that is currently under study, concerns the existence and nature of a phase transition, that is beleived to occur at higher densities.

References

1. The effect of dipolar forces on the structure and thermodynamics of classical fluids, P. I. C. Teixeira, J. M. Tavares and M. M. Telo da Gama, J. of Phys.: Condensed Matter 12, R411-R434 (2000)
2. Quasi-two-dimensional dipolar fluid at low densities: Monte Carlo simulations and theory, J. M. Tavares, J. J. Weis and M. M. Telo da Gama, Physical Review E 65, 61201 (2002); also published in the July 1st issue of Virtual Journal of Nanoscale Science and Technology (http:/www.vjnano.org/).