MODEL

The dipolar hard – sphere fluid (DHS) is a classical many body system formed by identical spheres carrying a central dipole.  In our studies both the 3-dimensional case (N  dipolar hard spheres in a cube) and the 2-dimensional case (N dipolar hard disks in a square – see fig.1) have been considered.

Fig.1 : Schematic picture of a dipolar hard sphere fluid. The arrows represent the central point dipoles of each particle.

Each particle  is caracterized by a dipole (a vector of strength  m , the dipole moment) and a diameter s.

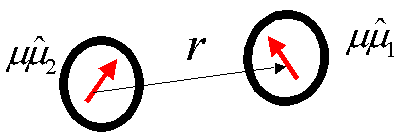
      A pair of particles interacts through a potential energy that is:

         (i)  infinity when the distance between the particles is less than their diameter s (meaning that the particles are hard and cannot overlap)

         (ii) equal to the dipolar interaction for distances ( r ) larger than  the particle diameter s: 

    This interaction is anisotropic: it depends not only on the relative orientation of the dipoles but also on the direction of the interdipolar vector. In the following figure we consider 4 dipole orientations for a pair of particles at contact and calculate their dipolar potential energy:

Potential Energy

2                        -1                     1                 -2 

The dipolar potential favours the “head to tail alignment” of the dipoles (the configuration with lower energy) and is also negative for paralell dipoles pointing in opposite directions. It can be shown that, as a consequence, the linear clusters of dipolar particles with lower energy are rings. Chains have also a low energy that, in the limit of large clusters, becomes equal to that  of rings.

                                                             RING                CHAIN

 When the thermal energy (kinetic energy) is much larger than the dipolar energy (potential energy), i.e. when the temperature is high,  the DHS behaves like an ideal gas  and no trace of the chain and ring structures is found. The DHS is in a regime where entropy dominates.   By contrast, when the temperature is very low, i.e. when the dipolar energy is much larger than the kinetic energy, one expects that all the particles in the gas form one or a few rings and chains. The DHS is then in a regime where energy dominates.