Gás de Rede

Introdução
Utilização
Questões
Breve Análise do Código
Extensões e variantes

Introdução

Este programa utiliza um modelo chamado gás de rede (ou "lattice gas") para demonstrar algumas características da transição de fase líquido vapor.

As partículas da substância são representadas por sítios (patches) ocupados e pretos. É possível, variar a quantidade de partículas (ou densidade, número de partículas por unidade de área) e a temperatura do sistema de forma independente. Em consequência, este programa vai permitir investigar o diagrama de fases densidade-temperatura do gás de rede que possui as mesmas características do diagrama de fases das substâncias simples correspondente às fases líquido e vapor.

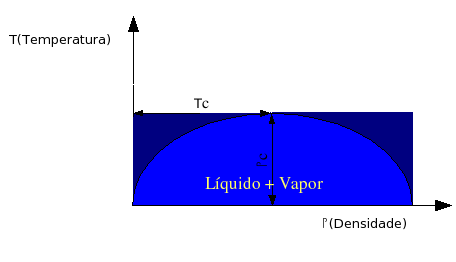
Legenda: Representação esquemática do diagrama de fases. Abaixo da temperatura crítica o estado de equilíbrio é o líquido a densidades elevadas e o gás a baixas densidades.Numa gama de densidades intermédia, delimitada pelas densidades de coexistência do líquido e do gás a essa temperatura (curva de coexistência) o estado de equilíbrio corresponde à coexistência entre os dois estados. Acima da temperatura crítica o estado estável é fluido com uma densidade que varia continuamente.

Início

Utilização

O objectivo deste programa é descobrir as configurações de equilíbrio (e a energia correspondente) do gás de rede para um par de parâmetros (densidade, temperatura).

Os agentes deste programa são apenas "patches" de dois tipos, ocupados (pretos) e desocupados (brancos). Cada par de patches vizinhos ocupados tem energia -1 e, consequentemente, a energia de uma configuração é igual ao simétrico do número de pares de patches vizinhos ocupados. Na versão aqui apresentada, cada “patch” tem 4 vizinhos (os sítios da rede mais próximos).

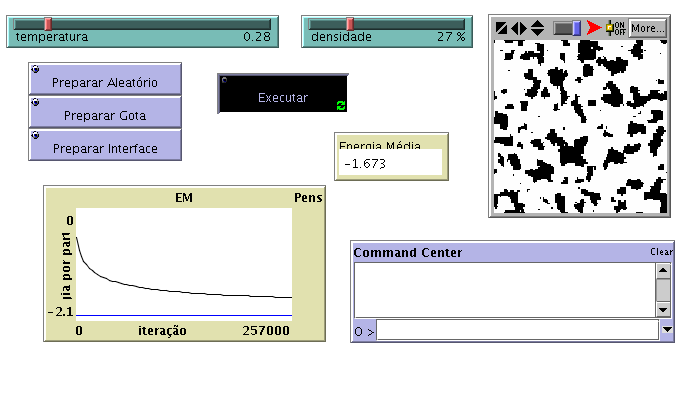
Depois de gerada uma configuração inicial, o programa procura as configurações de equilíbrio tentando movimentar partículas para sítios desocupados; i.e., tentando trocar patches ocupados com patches desocupados. Em cada iteração, são escolhidos aleatóriamente dois patches, um ocupado e outro desocupado. Para decidir se efectua ou não esta troca, o programa calcula a diferença de energia (DE) entre a configuração que resultaria da troca e a actual. Se esta diferença de energia for negativa (i.e. se da troca resultar uma diminuição da energia) então a nova configuração é aceite; se a diferença de energia for positiva a troca é efectuada com probabilidade p = exp(-DE/T).

Ao longo do seu funcionamento, o programa regista a energia média do sistema por partícula (ou seja, o número de pares de patches vizinhos ocupados dividido pelo número de patches ocupados).

O programa apresenta dois sliders: a densidade ou fracção de patches ocupados (em percentagem) e a temperatura.

Estes dois parâmetros podem ser variados de forma independente. No início da utilização deste programa devem escolher-se os valores destes parâmetros.

O estabelecimento da configuração inicial é feito utilizando um dos três botões de preparar.

Todos vão “criar” um número de patches ocupados proporcional à densidade: o Preparar Aleatório; distribui aleatóriamente esses patches sobre a rede;

o Preparar Gota; coloca esses patches num aglomerado no centro da rede.

o Preparar Interface; coloca esses patches num aglomerado na parte inferior da rede

O botão executar faz “arrancar” o programa, i.e., inicia a procura das configurações de equilíbrio tentando trocar patches ocupados e desocupados de posição

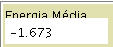
O “monitor” Energia Média; representa a energia do sistema por partícula para a configuração ilustrada.

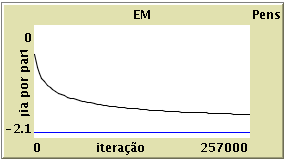
Existe um “plot” que representa em gráfico a energia por partícula em função do número de iterações.

Em resumo, para usar este programa dão-se os seguintes passos:

definição dos valores da densidade e da temperatura usando os respectivos “sliders”
escolha do tipo de condições iniciais (aleatórias, aglomerado ou interface)
observação, no plot e na janela gráfica, da evolução do sistema em direcção ao estado de equilíbrio.
os estados de equilíbrio são atingidos quando a energia começa a apresentar apenas pequenas oscilações em torno de um valor médio
para “parar” o programa pode carregar no botão «executar» ou escolher no menu principal as opções “tools – halt”.

Note que existe uma ligeira diferença técnica entre os dois “sliders”: a temperatura pode ser variada enquanto o programa corre, não se passando o mesmo com a densidade.

Início

Questões

1) Fixe a temperatura em 0.30 e a densidade em 10%. Corra o programa durante algum tempo para cada condição inicial, deixando a energia convergir para um valor estável. Observe a janela de representação gráfica das configurações, que deve ter o seguinte aspecto ( utilize screen-edge x e y =40, patch size=1 e font size=1).

Utilizando o Preparar Aleatório
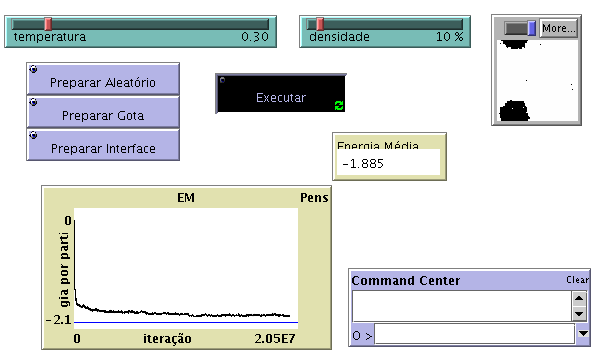
Utilizando o Preparar Gota
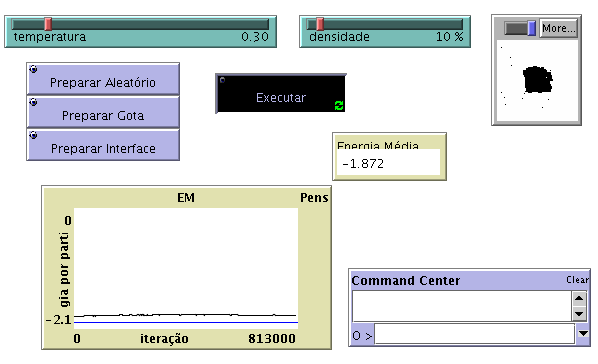
Utilizando o Preparar Interface

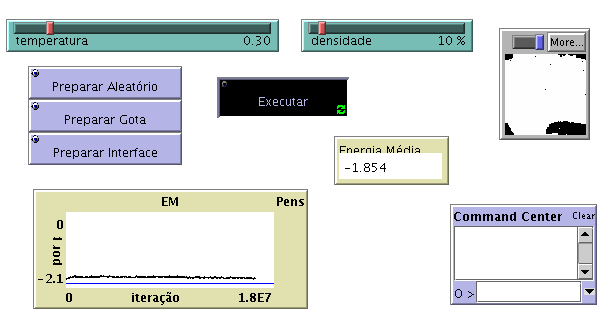
NOTA: Deveria ser obtida uma única gota quando se utiliza o Preparar Aleatório. No entanto, analisando os resultados é possível observar a formação de várias gotas. Seria necessário esperar mais tempo para que essas gotas se juntassem numa só.Nesta situação existe coexistência líquido vapor: o estado líquido corresponde à gota compacta de patches pretos; o estado gasoso aos patches pretos isolados.

2) Para a mesma densidade aumente a temperatura para 0.75. Verifique que neste caso não existe coexistência líquido vapor.Interprete os resultados obtidos em 1) e 2) em termos de minimização da energia e maximização da entropia.

3) Repita os procedimentos de 1) para as densidades: 30%, 50% e 70%. Relacione os resultados obtidos com o diagrama de fases do gás de rede.

4) Fixe uma densidade e uma temperatura. Compare a evolução da energia com as iterações para as duas escolhas de condições iniciais(Aleatório e Gota).Em qual das situações converge a energia mais rapidamente para o valor de equilíbrio?Porquê?

Gráficos obtidos para uma densidade de 30% e para uma temperatura de 0.60

Com o Preparar Aleatório
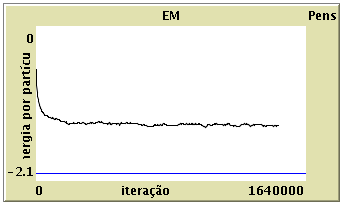
Com o Preparar Gota
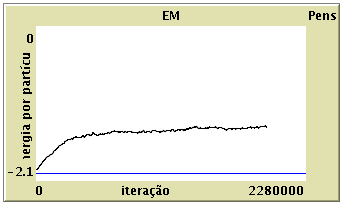
Com o Preparar Interface

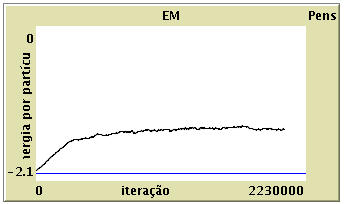
NOTA:A energia mínima por partícula corresponde a quatro (número máximo de primeiros vizinhos ocupados na rede quadrada) vezes a energia por partícula de um par de sítios ocupados(-1/2)

5) A energia (por partícula) pode variar entre -2 e 0. Tente escolher pares densidade/temperatura em que, na situação de equilíbrio, a energia se aproxime destes valores.

6) Percorra o diagrama de fases de forma sistemática a uma densidade constante (< 50%). Registe, para cada temperatura, o valor da energia no equilíbrio.

Sugestão:Traçar um gráfico da energia por partícula em função da temperatura.

7)Repita a questão 5 para os diferentes tipos de preparação, confronte os resultados e veja o que pode concluir

8)Fixe a densidade a 50% e percorra a temperatura (começe em 0.35) em passos de 0.05 analisando a evolução da estrutura do sistema. Verifique que à volta de T= 0.55 a estrutura é diferente da observada a temperaturas mais baixas e mais altas

Início

Breve Análise do Código

Conceito Geral

O funcionamento básico deste modelo resume-se à execução de iterações sucessivas sobre a configuração existente de gás (distribuição de patches ocupados). Cada iteração processa-se da seguinte forma: É seleccionado um patch aleatoriamente, e de seguida, também aleatoriamente, é seleccionado um patch de cor diferente, de maneira a obter-se um par de patches ocupado/desocupado. Depois, a diferença de energia E entre a configuração inicial e a possível configuração final resultante da troca é usada para se obter um limiar de probabilidade dado por exp(E/T), em que T é a temperatura do sistema. Este limiar é comparado com uma variável aleatória gerada para cada iteração (através de random-float 1.0) e, se superior, a troca é aceite.

Como consequência, se a troca resultar numa diminuição de energia, então E>0, ou seja, exp(E/T)>1, e a troca é sempre aceite.

Este procedimento é repetido até o utilizador o interromper desactivando o botão Executar.

Variáveis globais

Nome	Tipo	Descrição
iteracoes	global	Conta o número de iterações (tentativas de troca) já efectuadas.
energia	global	Energia média (por partícula) instantânea do sistema.
npo	global	Variável auxiliar inicializada com o valor constante *-2 count patches with [ pcolor = black ]**. Usada para calcular a energia por partícula.
noc	patch	Contém, para cada patch, o número de vizinhos desse patch que estão ocupados (0≤noc≤4).

Funções principais

Nome	Botão Associado	Domínio De Execução	Descrição
preparar-aleatorio	Preparar Aleatório	observer	Prepara a janela com uma distribuição aleatória de partículas sujeita ao valor da densidade.
preparar-gota	Preparar Gota	observer	Prepara uma distribuição contínua e regular (gota) centrada na janela sujeita ao valor da densidade.
preparar-interface	Preparar Interface	observer	Separa a janela em duas regiões separadas por um interface contínuo, de acordo com a densidade.
Executar	Executar (forever)	observer	A simulação corre enquanto este botão estiver premido.

Funções auxiliares

Nome	Domínio De Execução	Descrição
Trocar	observer	Função que tenta trocar um par de patches ocupado/desocupado definido pela função Executar.
preparar-grafico	observer	Inicializa o gráfico de energia média.
grafico	observer	Marca pontos no gráfico de energia média.

Código

Variáveis globais

globals [ iteracoes energia npo ]

patches-own [ noc ]

Funções principais

preparar-aleatorio

to preparar-aleatorio
  clear-all
  ask patches
  [ ifelse random-float 100 < densidade
    [ set pcolor black ]
    [ set pcolor white ] ]
  ask patches [ set noc count neighbors4 with [ pcolor = black ] ]
  set npo -2 * count patches with [ pcolor = black ]
  set energia sum values-from patches with [ pcolor = black ] [ noc ] / npo
  set iteracoes 0
  display
  preparar-grafico
  grafico
end

Este procedimento começa por inicializar a janela gráfica:

clear-all
ask patches [ ifelse random-float 100 < densidade [ set pcolor black ] [ set pcolor white ] ]

Limpando primeiro o estado do programa, e depois pedindo a todos os patches para que se tornem pretos (ocupados) ou brancos (desocupados) de acordo com uma variável aleatória gerada para cada patch, e cujo limiar de probabilidade é dado pelo slider densidade (expresso em %).

De seguida, inicializam-se todas as variáveis:

ask patches [ set noc count neighbors4 with [ pcolor = black ] ]
set npo -2 * count patches with [ pcolor = black ]
set energia sum values-from patches with [ pcolor = black ] [ noc ] / npo
set iteracoes 0

A primeira instrução deste bloco pede a cada patch para contar o número de vizinhos ocupados que possuí e guardar o valor na sua variável noc. As duas instruções seguintes contabilizam a energia potencial do sistema como a soma de todas as energias de ligação entre pares de patches vizinhos ocupados. O factor -2 que entra na variável (constante ao longo de cada simulação) npo deve-se ao facto das energias potenciais serem convencionalmente representadas por valores negativos e serve também para que cada par de patches seja contabilizado apenas uma vez. Finalmente, a última instrução inicializa o contador de iterações a zero.

Por fim, activa-se a actualização da janela gráfica (com a primitiva display, ver à frente), que pode ter sido desactivada por uma anterior execução do modelo, e inicializa-se o gráfico de energia média, marcando um primeiro ponto correspondente a esta configuração inicial:

display
preparar-grafico
grafico

preparar-gota

to preparar-gota
  locals [ lado ]
  clear-all
  set npo int (screen-size-x * screen-size-y * densidade / 100)
  ask patches [ set pcolor white ]
  set lado int ((sqrt npo - 1) / 2)
  ask patches with [ abs pxcor <= lado and abs pycor <= lado ] [ set pcolor black ]
  ask random-n-of (npo - (2 * lado + 1) ^ 2) patches with [ (abs pxcor = lado + 1 and
    abs pycor <= lado + 1) or (abs pxcor <= lado + 1 and abs pycor = lado + 1) ]
    [ set pcolor black ]
  ask patches [ set noc count neighbors4 with [ pcolor = black ] ]
  set npo -2 * npo
  set energia sum values-from patches with [ pcolor = black ] [ noc ] / npo
  set iteracoes 0
  display
  preparar-grafico
  grafico
end

A grande diferença deste procedimento relativamente ao anterior é a distribuição inicial de patches ocupados. Neste caso, começa-se por fazer npo igual ao número exacto de patches que devem estar ocupados de acordo com o slider densidade. Começa-se também com uma janela completamente preenchida com patches desocupados (brancos):

clear-all
set npo int (screen-size-x * screen-size-y * densidade / 100)
ask patches [ set pcolor white ]

De seguida, criam-se os patches ocupados em duas fases: Primeiro, cria-se um quadrado centrado na janela com o maior lado possível tal que todos os patches por ele contidos estejam ocupados. Segundo, os patches que sobram para perfazer o valor de npo são distribuídos aleatoriamente pela fronteira do quadrado já criado.

set lado int ((sqrt npo - 1) / 2)
ask patches with [ abs pxcor <= lado and abs pycor <= lado ] [ set pcolor black ]
ask random-n-of (npo - (2 * lado + 1) ^ 2) patches with [ (abs pxcor = lado + 1 and
abs pycor <= lado + 1) or (abs pxcor <= lado + 1 and abs pycor = lado + 1) ]
[ set pcolor black ]

As últimas 7 instruções são semelhantes às do procedimento anterior, servindo para inicializar as variáveis e o gráfico.

preparar-interface

to preparar-interface
  locals [ altura ]
  clear-all
  set npo int (screen-size-x * screen-size-y * densidade / 100)
  ask patches [ set pcolor white ]
  set altura int (npo / screen-size-x)
  ask patches with [ pycor < altura - screen-edge-y ] [ set pcolor black ]
  ask random-n-of (npo - altura * screen-size-x) patches with
    [ pycor = altura - screen-edge-y ] [ set pcolor black ]
  ask patches [ set noc count neighbors4 with [ pcolor = black ] ]
  set npo -2 * npo
  set energia sum values-from patches with [ pcolor = black ] [ noc ] / npo
  set iteracoes 0
  display
  preparar-grafico
  grafico
end

Semelhante ao procedimento anterior, excepto que a região preenchida é, desta vez, uma faixa que ocupa toda a largura da janela gráfica, na sua zona inferior:

set altura int (npo / screen-size-x)
ask patches with [ pycor < altura - screen-edge-y ] [ set pcolor black ]
ask random-n-of (npo - altura * screen-size-x) patches with [ pycor = altura - screen-edge-y ]
[ set pcolor black ]

Executar

to Executar
  locals [ p q ]
  without-interruption
  [ no-display
    set p random-one-of patches
    set q random-one-of patches
    ifelse pcolor-of p = black
    [ if pcolor-of q = white [ Trocar p q ] ]
    [ if pcolor-of q = black [ Trocar q p ] ]
    every 0.1
    [ display
      set energia sum values-from patches with [ pcolor = black ] [ noc ] / npo
      grafico ] ]
end

Este é o procedimento principal do modelo, que comanda a simulação. Estando associado a um botão do tipo forever, o procedimento executa repetidamente até que o botão Executar seja desactivado. Pode-se ver que o procedimento usa duas variáveis locais, p e q, e que as instruções estão todas contidas dentro de um bloco without-interruption. Vejamos primeiro o que esta e outras primitivas fazem.

Como já foi visto, o NetLogo possui vários contextos de execução, estando cada um associado a um agente (observer, turtle ou patch). Normalmente, todos os agentes que têm instruções para executar fazem-no em paralelo, ou seja, assim que um determinado agente executa uma instrução, outro agente passa a executar, mesmo antes do primeiro agente ter terminado todas as suas instruções, e assim sucessivamente (ver a secção do Apêndice que discute sincronização entre agentes para mais detalhes). A primitiva without-interruption serve então para definir ("proteger") um bloco de instruções que não pode ser interrompido (onde necessário), para que não possam ocorrer eventuais problemas de consistência. Esta primitiva faz isto parando a execução de todos os agentes excepto aquele que está actualmente dentro do bloco without-interruption [ instruções ... ] e até que todas as instruções nesse bloco tenham terminado. Isto tem também o efeito secundário de acelerar a execução do agente actual (uma vez que os outros são postos em espera), e é apenas para aproveitar esse efeito secundário que usamos esta primitiva neste caso, pois neste código não há possibilidade de ocorrerem falhas de consistência, sendo então que without-interruption não seria necessário em princípio.

A primitiva every tempo [ instruções ... ] serve para executar o bloco de instruções que contém a intervalos regulares, definidos pelo valor de tempo (em segundos). Ou seja, tempo é o intervalo de tempo mínimo que tem que existir para que uma nova execução do bloco de instruções seja permitida. Por exemplo, no caso utilizado, every 0.1 [ ... ] significa que as instruções contidas executam no máximo 10 vezes por segundo.

As primitivas display e no-display servem para activar/desactivar, respectivamente, a actualização da janela gráfica (activada por defeito). Isto pode ser útil para esconder passos intermédios em que apenas se vê o estado inicial e final após uma série de movimentos ou outras alterações sequenciais. Mais vulgarmente, desactiva-se a actualização da janela gráfica para que os cálculos internos do modelo possam correr mais rapidamente, uma vez que a actualização da janela consome muitos recursos de processamento. No caso deste modelo, a combinação da primitiva no-display no início juntamente com a primitiva display no interior do bloco every garante que a janela seja actualizada apenas 10 vezes por segundo em vez de continuamente, o que contribui significativamente para que o modelo corra a uma velocidade aceitável.

Estritamente falando, estas primitivas agora mencionadas são desnecessárias, uma vez que o modelo daria resultados completamente iguais sem as usar. No entanto, todas contribuem para aumentar significativamente a velocidade de execução do modelo.

Quanto às instruções responsáveis pela simulação propriamente dita, estas são muito simples: Limitam-se a escolher dois patches aleatoriamente (um atribuído à variável p e outro à variável q), e, no caso de terem cores diferentes, passá-los à função Trocar, que vai decidir se os patches serão trocados. É apenas necessário ter o cuidado de passar à função Trocar primeiro o patch ocupado (como primeiro parâmetro) e depois o livre (segundo parâmetro). É isto que faz o bloco ifelse:

set p random-one-of patches
set q random-one-of patches
ifelse pcolor-of p = black
[ if pcolor-of q = white [ Trocar p q ] ]
[ if pcolor-of q = black [ Trocar q p ] ]

O procedimento Executar é também responsável por manter actualizado o valor da energia média (na variável global energia), e por chamar o procedimento que desenha o gráfico. Mais uma vez, por razões de velocidade, isto é feito apenas 10 vezes por segundo ao incluír as instruções relevantes dentro do bloco every:

set energia sum values-from patches with [ pcolor = black ] [ noc ] / npo
grafico

Funções auxiliares

Trocar

to Trocar [ patch-ocupado patch-livre ]
  if random-float 1.0 < exp ((noc-of patch-livre - noc-of patch-ocupado) / temperatura)
  [ ask patch-livre [ ask neighbors4 [ set noc noc + 1 ] set pcolor black ]
    ask patch-ocupado [ ask neighbors4 [ set noc noc - 1 ] set pcolor white ] ]
  set iteracoes iteracoes + 1
end

O procedimento Trocar recebe dois parâmetros. Quando é invocado pelo procedimento Executar, é lhe passado um patch preto (ocupado) no primeiro parâmetro e um patch branco (livre) no segundo parâmetro. O procedimento Trocar acede às variáveis noc de cada um dos patches e usa-as para calcular a diferença de energia sofrida pelo sistema caso se efectuasse a troca entre os dois patches. Verifica-se facilmente que esta diferença de energia obtém-se subtraindo os números de patches vizinhos ocupados de cada um dos patches.

Esta diferença de energia (que pode ser positiva, zero, ou negativa) é dividida pelo valor da temperatura definido pelo slider correspondente (sempre positivo), e o resultado serve como argumento para a função exponencial, obtendo-se um valor estritamente positivo que vai ser comparado com uma variável aleatória obtida com a primitiva random-float. Este é um procedimento convencionalmente designado por algoritmo de Metropolis e é muitas vezes usado para estabelecer as probabilidades de transição de estados de sistemas discretos que possuem alguma medida (como a energia, neste caso) que dá uma ideia da distância a que o sistema se encontra do estado de equilíbrio compatível com a temperatura escolhida. A forma particular da função escolhida [exp(energia/temperatura)] é usada porque, quando o sistema atinge o equilíbrio, o seu comportamento (probabilidade de permanência em cada micro-estado particular) segue uma distribuição de probabilidades canónica, denominada distribuição de Boltzmann, e que obedece exactamente a esta forma.

Caso o procedimento decida trocar os dois patches (através do método descrito), isto é feito muito simplesmente mudando a cor de cada patch para a cor inversa (uma vez que as cores representam estados de ocupação) e actualizando o número de patches vizinhos ocupados para cada um dos 4 vizinhos de cada patch. Ou seja, é necessário incrementar a variável noc de cada um dos 4 patches vizinhos do patch que agora passou a estar ocupado (o que começou como patch-livre) e vice-versa para patch-ocupado. Em qualquer dos casos (quer haja ou não troca de patches), é sempre actualizada a variável iteracoes que conta o número de tentativas de troca.

preparar-grafico

to preparar-grafico
  set-current-plot "EM"
  set-current-plot-pen "eixo"
  auto-plot-off
  plotxy 0 -2
  plotxy 100000000 -2
  auto-plot-on
end

Este procedimento prepara o gráfico de energia média, desenhando uma linha de base no valor -2.0, que é o valor mínimo possível para a energia média. Este valor só pode ser atingido quando todos os patches ocupados estiverem rodeados apenas de patches ocupados. Ou seja, apenas pode ser atingido quando a densidade efectiva é 100%.

grafico

to grafico
  set-current-plot "EM"
  set-current-plot-pen "epp"
  plotxy iteracoes energia
end

Este procedimento simplesmente acrescenta um ponto ao gráfico, usando o valor de iteracoes como abcissa e energia como ordenada.

Inicio

Extensões e variantes

- Para verificar de forma visual que a quantidade de trocas de configuração aceites é muito maior quando a temperatura aumenta, pode "pintar" de uma terceira cor os "patches" ocupados que resultaram da troca com um patch desocupado.

- Construa um "reporter" que registe o número de pares de patches vizinhos ocupado-desocupado (por patch ocupado). Verifique se este parâmetro adicional pode ajudar à identificação da fase em que se encontra o sistema.

- Altere o programa de modo a que os patches vizinhos sejam oito (os quatro mais próximos da actual versão + os 4 seguintes em proximidade). Verifique que a única alteração relevante é a variação da temperatura crítica.

- Acrescente ao programa um campo gravítico, i.e., considere que a energia das partículas depende da sua altura (é tanto mais elevada quanto maior for a altura). Utilize um slider para poder controlar a intensidade deste campo e altere convenientemente o cálculo da diferença de energias entre configurações.iniciais.

Quais as principais alterações verificadas nos estados de equilíbrio a temperaturas elevadas e a temperaturas baixas?

Início