Research Investigação
Phenomenology of Supersymmetric Integer Charge Quark Theories
The Standard Model (SM) is a phenomenally successful theory, with precision measurements confirming two and three-loop calculations made in the framework of the Glashow-Weinberg-Salam model. And however the fact remains that there is very little direct experimental evidence confirming fractional electric quark charges. Integer Quark Charge (ICQ) theories were first proposed in the 60's by Han and Nambu [1], renormalisable versions first built by Pati and Salam shortly afterwards [2]. An interesting feature of these theories is that they perfectly mimic fractional quark charge (FCQ) models for all processes involving less than two photons. Witten recognised in 1977 [3] that two-photon processes were the ideal place to test the character of quark charges, namely the reaction
e+ e- → e+ e- q q,
as the resulting cross sections were predicted very differently in both theories. The problem with this picture is that low energy photon-photon collisions are dominated by non-perturbative physics, which drowns whatever conclusions one might make about the partons underlying the interaction. At LEP2 energies, however, the non-perturbative components – the so-called resolved processes, in which the photon fluctuates into a hadronic state before taking part in the interactions – are very small when compared to the perturbative processes.
Recently [4] several LEP collaborations have discovered that the predictions of the Standard Model seriously underestimate the results obtained in heavy-quark pair production via the two-photon channel. As may be appreciated in figure (1) a Next-to-Leading-Order (NLO) QCD calculation in the SM successfuly reproduces the total cross section for charm quark pair production (the upper solid line), for energies up to ~200 GeV.
It is a different matter altogether for bottom quark pair production – the NLO QCD calculation using state-of-the-art loop calculations and non perturbative calculations, is smaller by a factor of 3 than the experimental result. This is made all the more curious by the fact that at such high energies, and for quarks as heavy as the charm and bottom ones, perturbative QCD was expected to do a good job at reproducing these results. That such doesn't happen is a clear signal our understanding of these processes is faulty.
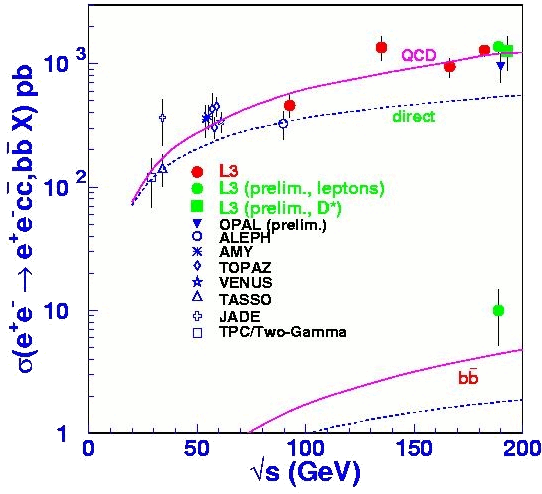
Figure 1: results from LEP collaborations on heavy quark pair production in two-photon collisions. The dotted lines represent the theoretical perturbative cross section, the solid lines are the full cross sections, including non-perturbative contributions [4].
Our basic hypothesis is that quarks do possess integer electric charges and that the cross sections for these reactions are almost entirely perturbative in nature. A simple study of ICQ theories reveals that vis à vis the FCQ result, the ICQ cross section for charm pair production in two-photon collisions should, at tree level, be 9/4 times bigger. Likewise, the ICQ cross section for bottom quark pair production is given by 9 times the FCQ one. These multiplicative factors have a simple origin, they arise from the fact quarks, in ICQ theories, have electric charges dependent on the colour index. An up type quark, for instance, has charge given by
Qu = (+1, +1, 0),
and a down-type one,
Qd = (0, 0, -1).
This differs substantially from FCQ theories where quarks have the same charge for each of their colours, +2/3 and -1/3 for up and down quarks, respectively. It is then very simple to show [5] that a factor of 9/4 arises for up quarks, and a factor of 9 for down ones.
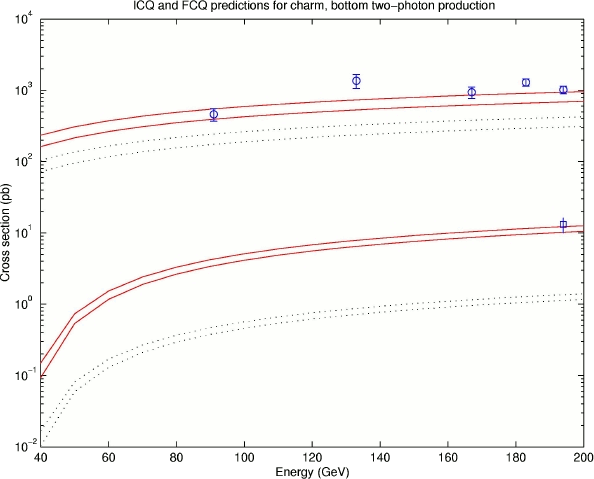
Figure 2: FCQ versus ICQ predictions for quark pair production via the two-photon channel. The dotted lines are the FCQ tree-level cross sections, the solid lines the ICQ ones. The bands correspond to different input quark masses [6].
Thus, if we calculate the FCQ cross section for charm and bottom pair production and multiply them by factors of 9/4 and 9 we obtain the ICQ predictions. The result of this exercice is in the figure (2) – the dotted lines are the FCQ cross sections (the lower line corresponds to lower quark masses, the upper to higher ones - the cross sections vary with the value of quark mass taken, we study the intervals 1.3 < mc < 1.7 GeV, 4.5 < mb < 5 GeV), the solid lines the ICQ ones, both computed at tree-level. The results are plain to observe – the ICQ theory not only reproduces the charm data as well as the SM, it succeeds where the SM fails – in correctly predicting the value of the bottom cross section [6].
One might dismiss this agreement as simple numeric coincidence, but the fact is that other observables are found to be in disagreement with the SM – and preliminary results [6] show that ICQ theories fit these data far better than the SM does. One such case is the inclusive production of charge pions in photon-photon collisions – the differential cross section of this process disagrees with its SM prediction by a factor of about 40 for very high values of the transverse momentum of the observed particles, as can be seen from the figure opposite. Similar discrepancies between the SM and data are found in the inclusive production of neutral pions and cahrged kaons via the two-photon channel at LEP2. These are especially embarrassing as they occur in a domain of energy where our understanding of the theory ought to be better.
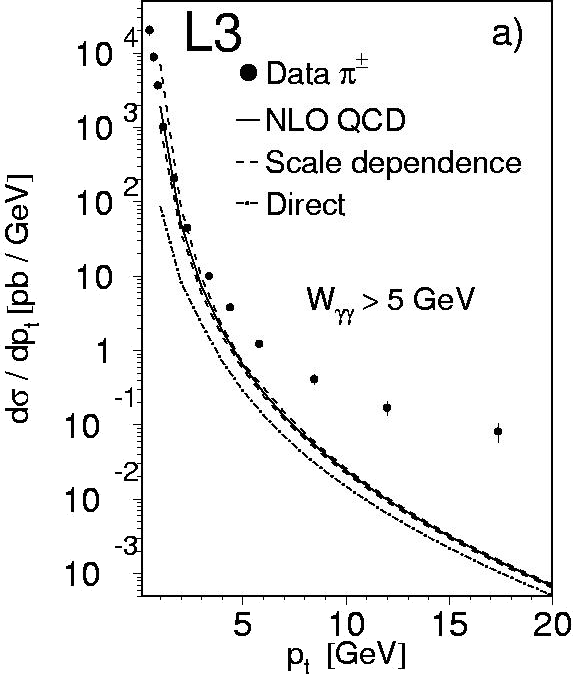
Figure 3: Differential cross section for inclusive production of charged pions in two-photon collisions at LEP2; the experimental data are well above the Standard Model theoretical prediction (full line, with all non-perturbative contributions included), there is a discrepancy of about 40 for the point with highest transverse momentum [4].
What we find is that ICQ theories fit these discrepancies very well. The theoretical calculation underlying these quantities involves quarks' fragmentation functions [7], which are non-perturbative in nature. As such we cannot deduce them from first principles and must use parametrisations taken from experiments. The results are strongly dependent on the choice of an arbitrary fragmentation scale but the improvement found in ICQ results over FCQ ones is dramatic.
Clearly the Standard Model , and the idea of quarks having fractional charges, cannot be abandoned on this evidence alone. For starters, though it is true ICQ theories mimic FCQ results very closely, we still don't kow for certain if all current experimental results can in fact be reproduced by ICQ models. And, of course, we have no idea what ICQ model to choose, there are many possible (all of them sharing the quark charge assignements described above). We built one particular such model, based on a supersymmetric theory with the SM's gauge group, but where the colour SU(3) is broken via a generalised Higgs-Mechanism by giving non-zero vaccuum expectation values to the scalar partners of the top quark [5]. It is an interesting attempt, but a great deal of work needs to be done before it is aparent that this theory manages to describe high energy physics phenomena in an acceptable manner. But the success of ICQ models in fitting the experiments where the SM fails so immensely is, we believe, reason enough to give some thought to the idea that perhaps quarks do, after all, have integer electric charges.
References
-
- M. Han and Y. Nambu, Phys. Rev. B139 (1965) 1006.
-
- J.C.Pati and A. Salam, Phys. Rev. D8 (1973) 1240.
-
- E. Witten, Nucl. Phys. B120 (1977) 189.
-
- OPAL collaboration, Eur. Phys. Jou. C14 (2000) 579;
- L3 collaboration, Phys. Lett. B503 (2001) 10; B524 (2002) 44; B554 (2003) 105.
-
- P.M. Ferreira, hep-ph/0210024, submitted to Nuclear Physics B.
-
- P.M. Ferreira, hep-ph/0209156, submitted to Physical Review Letters.
-
- B.A Kniehl et al, Nucl. Phys. B582 (2000) 514.
