Fractais Geométricos

Introdução
Alguns fractais, como os exemplos deste programa, possuem auto-semelhança exacta, isto é, têm sempre o mesmo aspecto visual independentemente da escala a que os observamos, porque o todo é exactamente igual à ampliação de uma das partes. Esta propriedade resulta do facto de serem construídos pela iteração 'ad infinitum' da mesma regra de construção.
Muitas formas na natureza são aproximadas por esta geometria. No entanto, os fractais apresentados neste programa não foram inventados para simular as propriedades de padrões naturais, mas sim para mostrar que a matemática continha mais objectos para além das curvas e superfícies regulares da geometria tradicional.
Considere o exemplo da famosa curva de Koch, criado em 1904 pelo matemático sueco Helge von Koch. Começa-se com um segmento de recta. Ao objecto inicial da construção chama-se "iniciador". De seguida divide-se o segmento inicial em três segmentos iguais. Depois disto substitui-se o terço do meio por um triângulo equilátero tirando-lhe a sua base. Neste momento completou-se a construção da unidade fundamental, o "gerador". A iteração deste processo consiste em aplicar a mesma regra a cada um dos segmentos de recta que resultam da iterada anterior, como se ilustra na figura. A curva de Koch é o objecto que se obtem no limite em que o número de iterações tende para infinito.
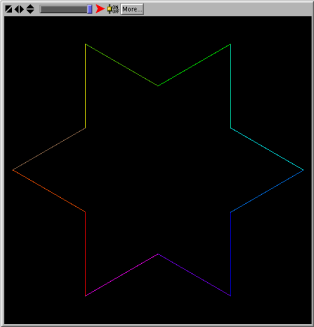
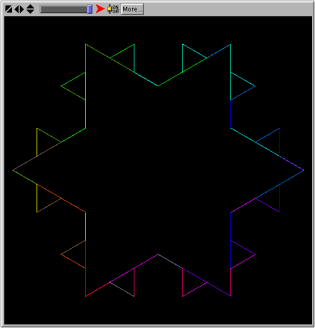
A auto-semelhança é um ingredientes do processo de construção. Cada segmento de recta contido na iterada k está reduzido por um factor de 3 em relação aos segmentos de recta que compõem a iterada anterior, e cada um dos quatro troços que compõem a iterada k é uma cópia, reduzida por um factor 3, de toda a estrutura da iterada imediatamente anterior.
Por isso, o objecto que resulta da passagem ao limite deste processo recursivo é exactamente auto-semelhante, é igual a uma cópia ampliada dos elementos que o constituem. Este objecto exótico tem o nome de curva, mas é uma curva que não contem nenhum segmento de recta e não pode ser diferenciada em nenhum dos seus pontos (é uma curva em que todos os pontos são "bicos").
InícioUtilização
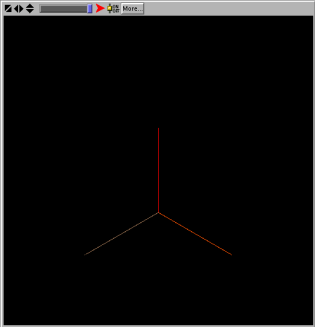
O programa permite seleccionar a construção de diferentes fractais geométricos. Por exemplo, para gerar a Árvore de Sierpinski, começa-se por escolher um ponto no plano e desenha-se três segmentos de recta desde esse ponto até aos vértices de um triângulo equilátero centrado no ponto inicial.
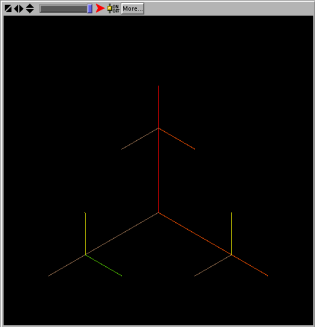
A segunda iteração do processo obtem-se aplicando a mesma operação sobre os vértices do triângulo considerados como novos pontos iniciais, e tomando segmentos de recta de comprimento metade dos da iteração anterior. A Árvore de Sierpinski é o fractal que resulta de iterar indefinidamente esta regra de construção.
Pode ver este procedimento posto em prática seleccionando a Árvore de Sierpinski e pressionando vezes sucessivas o botão "Desenhar uma iteracao". Pressionando este botão executa-se uma só vez a regra usada para a construção do fractal seleccionado. O botão "Desenhar" ("forever button") executa exactamente o mesmo procedimento que "Desenhar uma iteracao", mas executa-o até o utilizador voltar a pressioná-lo.
O botão quadrado de Sierpinski utiliza uma regra similar a esta com outra simetria. Premindo o botão Quadrado de Sierpinski 2 segue-se um esquema de desenho do fractal ligeiramente diferente do anterior. A ideia é dividir o quadrado inicial em nove quadrados iguais, retirar o do meio e aplicar indefinidamente este procedimentos ao quadrados restantes ao fim de cada iteração. Este é também um dos métodos de obtenção do Triângulo de Sierpinski. Finalmente, o programa permite ainda gerar a ilha de Koch, uma variante da curva de Koch.
O utilizador pode modificar o aspecto visual do seu fractal escolhendo a cor da primeira turtle criada ("cor-inic"). As turtles das gerações seguintes terão uma cor que corresponde à cor da sua "progenitora" incrementada de "cor-incremento" (ver representação numérica das cores no manual do utilizador).
Desta maneira, o código de cores permite visualizar o resultado das sucessivas iterações da regra de construção.
A interface apresenta ainda o botão "Exportar Mundo", que serve para armazenar num ficheiro o padrão gerado na janela. Utilizaremos esta funcionalidade para importar as imagens dos fractais geométricos para o programa de cálculo da dimensão de contagem de caixas.
InícioQuestões
1) Para se criar o Quadrado de Sierpinski o método utilizado foi o mesmo que para a Árvore, só que a regra mudou. Qual será a regra usada?
2) Qual é o limite a partir do qual a figura não se altera com sucessivas iterações da regra? Faça uma estimativa do número de iterações correspondente.
3) Note a auto-semelhança dos objectos a cada iteração. Iterando um número finito de vezes, notar-se-ía alguma diferença entre uma ampliação de uma parte da figura e toda a figura?
4) Quais são as diferenças entre o Triângulo e a Árvore de Sierpinski e entre o Quadrado de Sierpinski 2 e o Quadrado de Sierpinski ?
5) Note que o número de turtles em cada iteração vai sempre aumentando de um factor constante. Determine esse factor e preveja o o número de turtles numa iterada qualquer n. Relacione este cálculo com a taxa de aumento do aumento exponencial do tempo de desenho com n.
Início
Breve Análise do Código
Conceito Geral
Neste modelo começamos por definir para cada tipo de fractal uma função de preparação e outra de iteração para cada um dos tipos de fractal: ArvoreSierpinski, koch ou QuadradoSierpinski.
A primeira função limpa e inicializa as variáveis de acordo com o fractal pretendido, e de seguida cria uma turtle.
A segunda função itera o fractal de acordo com as regras correspondentes ao tipo de fractal escolhido.
Em cada iteração cria-se na posição das últimas tartarugas N novas tartarugas e de seguida, rodando-as e movendo-as de acordo com as regras do fractal traçam N novas linhas desde a posição das tartarugas da iteração anterior até às posições correspondentes à nova iteração.
De forma a poder criar novas turtles apenas nas posições das turtles da última iteração, definiu-se uma propriedade nova das turtles (nova?) que quando se encontra verdadeira (true) corresponde às turtles da iteração anterior. De cada vez que se itera o fractal, as turtles com a propriedade nova? = true passam a false e criam-se N turtles novas com a propriedade nova? = true.
Variáveis globais
| turtles,nova? | serve para manter um registo da últimas turtles criadas. |
| Qsierpinski?,Qsierpinski2?,Asierpinski,koch? | servem para escolher o tipo de fractal que se pretende gerar |
| comp | define o comprimento da linha que cada tartaruga irá traçar numa dada iteração e é actualizada de iteração em iteração |
| primeira-passagem? | utilizada para indicar caso se esteja a efectuar a primeira iteração. |
| N | utilizada na geração do Quadrado de Sierpinski para manter a comprimento do lado do quadrado. |
| cor | mantem a cor da última iteração |
Funções principais
| desenhar | chama a função iterativa correspondente ao fractal escolhido |
Funções auxiliares
| t | para todas as turtles antigas cria uma nova turtle |
| dir rot | roda todas as tartarugas antigas rot graus para a direita |
| esq rot | roda todas as tartarugas antigas rot graus para a esquerda |
| frente p | move as turtles antigas para a frente p passos traçando uma linha com a cor da turtle ao longo da trajectoria |
| salta p | move as turtles antigas para a frente p passos mas sem traçar linha |
| m | mata todas as turtles antigas |
| muda_cor | chamada de iteração em iteração para incrementar a cor das turtles |
| exportarmundo | exporta a imagem do fractal para um ficheiro que depois será utilizado no programa de cálculo da dimensão |
Código
Variáveis Globais
Começamos por definir uma propriedade adicional das turtles "nova?" e declarar as variáveis globais utilizadas neste programa.
turtles-own ;variável das turtles que indica se cada uma foi ou não criada na iteração corrente [ nova? ] globals [ comp ;comprimento Qsierpinski? ; Qsierpinski2? ; Asierpinski? ; koch? ;;indicam a opção do utilizador quanto ao fractal a desenhar primeira-passagem? N ; variável auxiliar (indica o número de patches de um lado do quadrado) cor ; mantem a cor da última iteração ]
Funções principais
desenhar
A função desenhar exposta a seguir, apenas chama a função iterativa correspondente ao fractal escolhido. Avisando o utilizador caso não tenha sido selecionado nenhum tipo de fractal. Avisando tambem caso a resolução máxima tenha sido atingida para o fractal do quarado de Sierpinski.
;procedimento que é executado sempre que se pressiona Desenhar uma iteração ou Desenhar
to desenhar
if Asierpinski? = 0 and koch? = 0 and Qsierpinski? = 0 and Qsierpinski2? = 0
[ user-message "Escolha um fractal!" stop ]
ifelse (Asierpinski?)
[ ArvoreSierpinski ]
[
ifelse (koch?)
[ IlhaKoch ]
[
ifelse (Qsierpinski?)
[ QuadradoSierpinski ]
[
;Se N for menor que 1 atingiu-se a resolução máxima deste programa
if 1 > N [ user-message "Atingiu a resolução máxima" stop ]
QuadradoSierpinski2
]
]
]
end
Funções auxiliares
t
;para cada turtle antiga, na iteração corrente, cria uma turtle nova e
;inicializa a sua variável nova? com o valor lógico verdadeiro
to t
ask turtles with [ not nova? ]
[
set color cor
hatch 1 [ set nova? true ]
]
end
muda_cor
;muda a cor das tartarugas de iteração em iteração, de acordo
;com o incremento
to muda_cor
set cor cor + cor-incremento
if cor = black
[ set cor cor + cor-incremento ]
ask turtles with [ nova? ]
[ set color cor ]
end
dir
;roda cada turtle com nova? = falso (isto é que não foi criada durante a presente iteração) ;gr graus à direita to dir [ gr ] ask turtles with [ not nova? ] [ rt gr ] end
esq
;cada turtle com nova? = falso vira gr graus à esquerda to esq [ graus ] ask turtles with [ not nova? ] [ lt gr ] end
frente
;move todas as turtles com nova? = falso em frente o numero de passos ;dado no argumento to frente [ passos ] ask turtles with [ not nova? ] [ fd passos ] end
salta
;move todas as turtles com nova? = falso em frente o numero de passos ;dado no argumento mas sem pintar os patches por debaixo to salta [ passos ] ask turtles with [ not nova? ] [ pu fd passos pd ] end
m
;mata todas as turtles não novas (i.e. com a variável nova? igual a falso) to m ask turtles with [ not nova? ] [ die ] end
exportarmundo
Por fim temos uma função que exporta a imagem do fractal para um ficheiro que depois será utilizado no programa de cálculo da dimensão.
;exporta o mundo (escreve o valor de todas as variáveis) ;para um ficheiro de nome nomeficheiro to exportarmundo locals [nomeficheiro] set nomeficheiro user-input "Nome do ficheiro da saída:" export-world nomeficheiro end
Funções da Árvore de Sierpinski
Para cada tipo de fractal definimos adiante uma função "setup" e uma função de iteração (cujo nome é o do fractal)
;inicializa as variáveis necessárias para seguidamente se efectuar o desenho da Árvore de Sierpinski
to AsierpinskiSetup
ca
crt 1
set cor cor-inic
ask turtles
[
set shape "line"
set color cor-inic
setxy 0 -70
set heading 0
pd
]
set comp 140
set Asierpinski? true ;indica a opção do utilizador quanto ao objecto a desenhar
set koch? false
set Qsierpinski? false
set Qsierpinski2? false
end
Na função setup da arvore de sierpinski, é criada uma tartaruga inicializando-se a sua cor. E por fim inicializa-se tambem a variavel comprimento e acertam-se as variáveis que escolhem o tipo de gráfico a desenhar.
to ArvoreSierpinski
;a cada nova iteração, as turtles existentes passam a antigas para essa iteração
ask turtles [ set nova? false pd ]
repeat 3 ;regra de construção
[
frente comp
t
dir 180
salta comp
dir 180
dir 120
]
muda_cor
set comp (comp / 2)
m
end
Na função de iteração da árvore de sierpinski, em cada iteração alteramos a propriedade nova? das turtles igualando-a false. De seguida movemos as tartarugas antigas em frente traçando uma linha de comp passos, chamando a função t criam-se N novas turtles, rodamo-la para a direita 180°, com o comando salta deslocamos as turtles antigas (sem traçar qualquer linha) em frente comp passos. E de seguida rodam-se as turtles de novo por 300° para a direita.
Funções da Ilha de Koch
Repete-se 3 vezes as instruções anteriores, actualiza-se o comprimento dos passos a dar pelas turtles. E por fim eliminam-se todas as tartarugas não criadas nessa iteração com o comando m.
;inicializa as variáveis necessárias para seguidamente se efectuar o desenho da Ilha de Koch
to kochSetup
ca
crt 1
set cor cor-inic
ask turtles
[
set shape "line"
set color cor-inic
setxy -121 -210
set heading 0
pd
]
set comp 140
set Asierpinski? false
set koch? true
set Qsierpinski? false
set Qsierpinski2? false
set primeira-passagem? true
end
Prepara-se da mesma forma o fractal de koch, embora para posições iniciais diferentes da turtle
to IlhaKoch
;a cada nova iteração, as turtles existentes passam a antigas para essa iteração
ask turtles [ set nova? false pd ]
ifelse (primeira-passagem?)
[
set primeira-passagem? false
;na primeira passagem por este procedimento estas regras são executadas 3 vezes
;para que se obtenha a forma de ilha
repeat 3
[
t frente comp esq 60 t frente comp dir 120 t frente comp esq 60 t frente comp dir 120
]
]
[ ;note que estas regras são as mesmas que as anteriores, só que agora só são executadas uma vez
t frente comp esq 60 t frente comp dir 120 t frente comp esq 60 t frente comp dir 120
]
muda_cor
set comp (comp / 3)
m
end
Neste caso faz-se uso da variável global primeira-passagem? para na primeira passagem se repetirem 3 vezes as regras de actualização
Em cada actualização cria-se na posição das turtles antigas uma turtle nova e traçando a linha de koch, criam-se mais 2 tartarugas em cada vértice, obtendo-se assim passo a passo o fractal de koch
Funções do Quadrado de Sierpinski
Como nos outros fractais, este tambem tem as funções de preparação e de iteração.
;inicializa as variáveis necessárias para seguidamente se efectuar o desenho do quadrado de Sierpinski
to QsierpinskiSetup
ca
crt 1
set cor cor-inic
ask turtles
[
set shape "line"
set color cor-inic
setxy 0 0
set heading 0
pd
]
set comp 128
set Asierpinski? false ;indica a opção do utilizador quanto ao objecto a desenhar
set koch? false
set Qsierpinski? true
set Qsierpinski2? false
end
to QuadradoSierpinski
ask turtles
[ set nova? false pd ]
ask turtles[ set heading 0 ]
repeat 4 ;regra de construção. Para se perceber como a regra foi refinada apresenta-se
[ ;a versão antiga, está comentada e apresenta-se a versão actual.
;Experimente a descomentar essas duas linhas e
;comentar as seguintes indicadas por ; à direita
;frente comp
salta comp / 2 ;
frente comp / 27 ;
salta comp / 27 ;
frente comp / 27 ;
salta comp / 9 ;
frente comp / 27 ;
salta comp / 27 ;
frente comp / 27 ;
salta comp / 6 ;
t
dir 180
salta comp
esq 135
;frente (comp * sqrt 2)
salta (comp * sqrt 2) / 2 ;
frente (comp * sqrt 2) / 27 ;
salta (comp * sqrt 2) / 27 ;
frente (comp * sqrt 2) / 27 ;
salta (comp * sqrt 2) / 9 ;
frente (comp * sqrt 2) / 27 ;
salta (comp * sqrt 2) / 27 ;
frente (comp * sqrt 2) / 27 ;
salta (comp * sqrt 2) / 6 ;
t
dir 180
salta (comp * sqrt 2)
esq 135
]
muda_cor
m
set comp comp / 3
end
Neste caso as turtles desenham os quadrados mais pequenos deslocando-se dos vértices do quadrado exterior para os quadrados mais pequenos e de seguida, percorrendo o lado dos quadrados correspondente a essa iteração. A variável comp é neste caso utilizada para o lado do quadrado e é reduziada para um terço de iteração em iteração.
Funções do Quadrado de Sierpinski 2
Para esta versão do quadrado de Sierpinski, em vez de se implementar usando turtles, utilizou-se as patches para obter uma variação.
Assim, o modelo começa por pintar um quadrado maior e ir sucessivamente retirando (pintando da cor preta) quadrados mais pequenos de acordo com as regras de iteração.
;Para o desenho do Quadrado de Sierpinski 2 o procedimento usado
;é diferente do procedimento usado anteriormente
;aqui não se faz uso do agente turtles
;inicializa as variáveis necessárias para seguidamente
;se efectuar o desenho do quadrado de Sierpinski
to QsierpinskiSetup2
ca
ask patches with[ 121 > pxcor and 121 > pycor and pxcor > -121 and pycor > -121 ]
[
;pinta o quadrado inicial, tem um lado de 243=3^5 para
;que se possa chegar à resolução do patch (=pixel)
set pcolor cor-inic
]
set comp 81 ;lado de cada quadrado em que se dividiu o quadrado maior
set N 81 ;indica o número de patches do lado do quadrado da maior divisão pretendida
;no início é 81 pois não se quer fazer divisão nenhuma
set Asierpinski? false
set koch? false
set Qsierpinski? false
set Qsierpinski2? true
end
to QuadradoSierpinski2
;Função recursiva que dado a posição do quadrado e lado, desenha todos os outros quadrados
DesenhaNivelN (- 121) (- 121) comp
;passa-se para uma divisão maior, ou seja, um lado do quadrado menor
set N N / 3
end
;função recursiva que se chama a ela própria até "comprini" (comprimento inicial) ser igual a N
to DesenhaNivelN [ pxcorini pycorini compini ]
ifelse N = compini
[
;se os dois comprimentos forem iguais então a partição pretendida
;foi atingida e pinta o quadrado central
qDesenha pxcorini pycorini compini
]
[
;se o comprimento não foi atingido chama-se novamente
;nos quadrados mais pequenos (excepto no central)
DesenhaNivelN pxcorini pycorini (compini / 3)
DesenhaNivelN (pxcorini + compini) pycorini (compini / 3)
DesenhaNivelN (pxcorini + 2 * compini) pycorini (compini / 3)
DesenhaNivelN pxcorini (pycorini + compini) (compini / 3)
DesenhaNivelN (pxcorini + 2 * compini) (pycorini + compini) (compini / 3)
DesenhaNivelN pxcorini (pycorini + 2 * compini) (compini / 3)
DesenhaNivelN (pxcorini + compini) (pycorini + 2 * compini) (compini / 3)
DesenhaNivelN (pxcorini + 2 * compini) (pycorini + 2 * compini) (compini / 3)
]
end
;dado um quadrado cujas coordenadas do canto inf. esq. são (qpxcor,qpycor) e
;o cujo lado é qcomp, esta função divide-o
;em nove quadrados iguais e pinta de negro o quadrado do meio
to qDesenha [ qpxcor qpycor qcomp ]
ask patches with [ pxcor >= (qpxcor + qcomp) and
(2 * qcomp + qpxcor) > pxcor and
pycor >= (qpycor + qcomp) and
(2 * qcomp + qpycor) > pycor ]
[ set pcolor black ]
end
Início
Variantes e Extensões
Experimente fazer os seus próprios fractais!
Para isso crie um botão (análogo aos existentes) que inicializa as variáveis necessárias para desenhar o seu fractal. De seguinda escreva uma função onde estarão as regras para a construção do seu fractal e coloque-a no procedimento Desenhar.
Construa as suas regras com as funções já criadas ou com outras que crie (p.e. frente 5 dir 90 salta 3 m). Basta seguir o exemplo dado pelo próprio programa.
Em baixo está a regra que cria o fractal Recobrimento Universal da Figura Oito. Experimente esta!
. Passo 0
|
|
|
______________ Passo 1
|
|
|
|
__|__
|
|
__|___________|__ Passo 2
| | |
|
__|__
|
Procure outros fractais e tente representá-los usando as regras deste programa ou outras.
Início
©opyright 2004, Centro de Física Teórica e Computacional