Predador-Presa

Introdução
Este modelo simula a coexistência de duas espécies, predadores e presas. A inicialização, execução e paragem de uma simulação faz-se da maneira descrita no módulo BICHOS. Também como nesse módulo, o selector COMPETICAO? activa ou desactiva o efeito de competição pelos mesmos recursos: Quando o selector está "on", uma sardinha ou um tubarão que ocupe um "patch" sobrelotado, isto é, ocupado por mais do que um indivíduo da mesma espécie, tem uma certa probabilidade de morrer. Essa probabilidade é controlada pelos cursores COMPETICAO-SARDINHAS e COMPETICAO-TUBAROES.
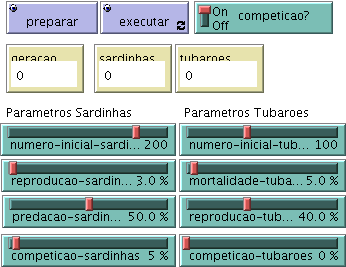
Sardinhas e tubarões deslocam-se aleatoriamente na janela gráfica, passando de um "patch" para um dos "patches" vizinhos em cada unidade de tempo. À parte o efeito de competição, a dinâmica de cada uma das populações é regulada pelos efeitos dos encontros predador-presa, e pela natalidade e mortalidade de cada espécie isolada. Para as sardinhas, a taxa de natalidade é regulada no cursor REPRODUCAO-SARDINHAS, e consideramos que a principal causa de mortalidade é serem vítimas dos tubarões. A probabilidade de, dado um encontro, uma sardinha ser comida é regulada no cursor PREDACAO-SARDINHAS.
Os tubarões têm uma taxa de mortalidade regulável com o cursor MORTALIDADE-TUBAROES, e reproduzem-se só se conseguirem caçar. Por isso, a reprodução dos tubarões é condicionada a um encontro predador-presa, e pode ocorrer com uma certa probabilidade, regulável com o cursor REPRODUCAO-TUBAROES. Tal como no módulo BICHOS, a reprodução significa a criação de um novo indivíduo num "patch" vizinho do progenitor.
Existem ainda dois cursores que estipulam a quantidade inicial de indivíduos de cada espécie.
InícioUtilização
Com o selector COMPETICAO? em "off", este modelo corresponde a uma versão discretizada e espacial do modelo predador-presa de Lotka-Volterra. Os únicos parâmetros do modelo são a taxa de reprodução das sardinhas, a taxa de mortalidade dos tubarões, a probabilidade de que um encontro seja mortal para uma sardinha e a taxa de reprodução dos tubarões dado um encontro. A simulação exibe durante algum tempo as oscilações características do modelo de Lotka-Volterra, no entanto a dinâmica é instável, a amplitude das oscilações aumenta e as flutuações acabam por resultar na extinção de uma das espécies.
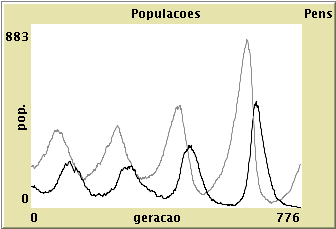
Com o selector COMPETICAO? em "on", o modelo usa mais dois parâmetros, que regulam a importância do termo logístico, ou seja, a maneira como a escassez de recursos se manifesta na mortalidade, em cada uma das espécies.
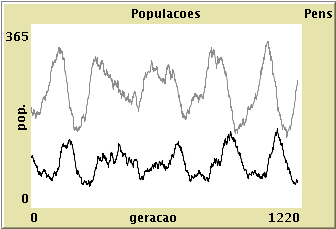
Tal como no modelo BICHOS, a competição dentro de cada espécie estabiliza a dinâmica, impedindo oscilações de grande amplitude nas populações. Neste regime, as flutuações estocásticas sobrepõem-se a um padrão regular de oscilações característico dos modelos de Lotka-Volterra, com um período bem definido e um desfasamento de um quarto de ciclo entre as duas populações.
InícioQuestões
1. Considere o modelo sem competição (selector COMPETICAO? em "off").
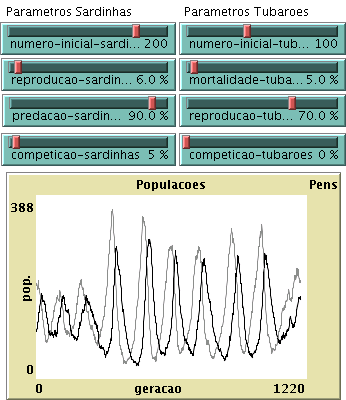
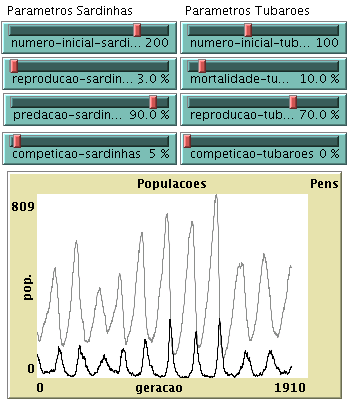
a) Corra a simulação para a seguinte escolha de parâmetros: Número inicial de sardinhas, 200; número inicial de tubarões, 100; taxa de reprodução das sardinhas, 3%; taxa de mortalidade dos tubarões, 5%; taxa de predação de sardinhas, 90%; e taxa de reprodução dos tubarões, 70%. A que se deve o desfasamento entre as oscilações do número de sardinhas e as oscilações no número de tubarões?
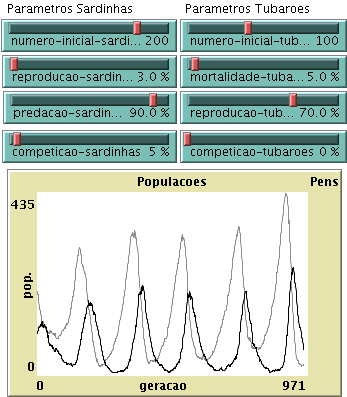
b) Corra agora a simulação com taxa de predação de sardinhas a 40%, e os mesmos valores do caso anterior para os outros parâmetros. Como explica que a extinção das sardinhas seja mais provável neste segundo caso?
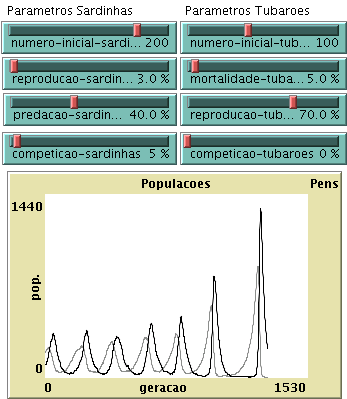
c) Procure estabilizar a simulação variando aqueles 6 parâmetros, e observe o efeito de cada um deles.
2. Considere agora o modelo com competição (selector COMPETICAO? em "on").
a) Observe a evolução da população experimentando pôr alternativamente COMPETICAO-SARDINHAS e COMPETICAO-TUBAROES com valores pouco maiores do que zero. Qual dos efeitos é mais eficaz para estabilizar a dinâmica global? Porquê?
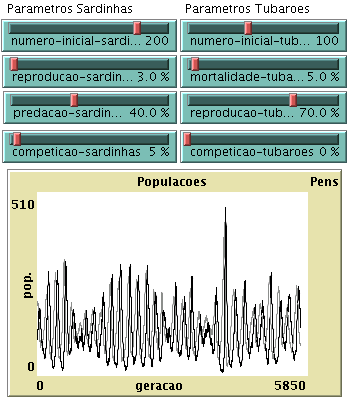
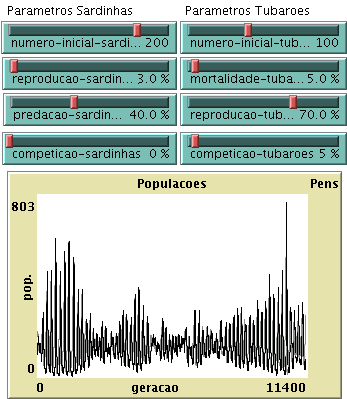
b) Tome os parâmetros indicados em 1.a), juntamente com 5% para a taxa de competição entre sardinhas e 0% para a taxa de competição entre tubarões. Deixe evoluír o sistema e faça uma estimativa do período das oscilações. Aumente para o dobro, separadamente, a taxa de reprodução das sardinhas, a taxa de mortalidade dos tubarões, e as duas em conjunto. Observe o efeito destas modificações no período das oscilações.
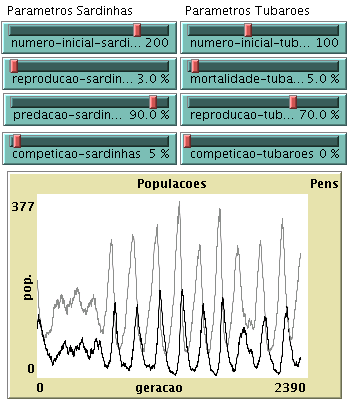
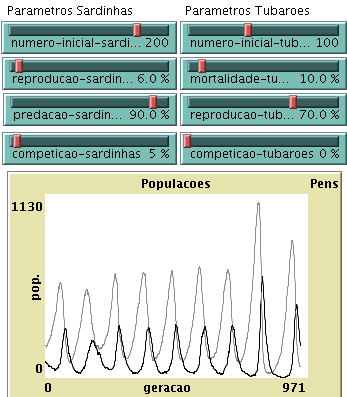
c) Analise agora o efeito das mesmas variações de parâmetros no valor médio das populações de cada uma das espécies.
d) A partir dos valores finais usados em 2.b) e 2.c), varie agora o valor dos parâmetros PREDACAO-SARDINHAS e REPRODUCAO-TUBAROES, tomando por exemplo 50% e 40%, respectivamente. O período das oscilações varia significativamente? E o valor médio das populações de cada espécie?
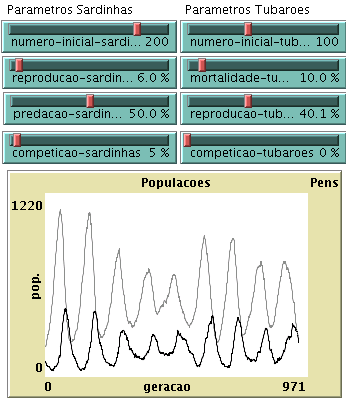
Início
Breve Análise do Código
Conceito Geral
Neste modelo, duas espécies (breeds) de turtles, sardinhas e tubaroes, deslocam-se na janela gráfica de maneira aleatória, controlados pelo procedimento movimento. Além disso, cada indivíduo interage com a sua própria espécie, e com a espécie oposta.
Uma causa de mortalidade tanto para tubarões como sardinhas é a colisão com elementos da sua própria espécie, devido à competição pelos mesmos recursos. Essa competição é mediada pelos procedimentos colisao-tubaroes e colisao-sardinhas, respectivamente.
As sardinhas reproduzem-se através do procedimento reproduzir-sardinhas. Os tubarões caçam sardinhas (procedimento apanhar-sardinhas), podendo reproduzir-se quando o fazem. Os tubarões podem também morrer isoladamente, de "causas naturais", através do procedimento morte.
Variáveis globais
| geracao | contador global de iterações |
| sardinhas, tubaroes | espécies de turtles usadas |
| sardinhas: apanhada? | variável de sincronização que impede que a mesma sardinha seja capturada por mais que um tubarão |
Funções principais
| preparar | prepara o modelo com os números especificados para cada espécie, distribuíndo os indivíduos aleatoriamente |
| executar | função que implementa cada iteração do modelo |
Funções auxiliares
| movimento | roda a turtle aleatoriamente entre 0 e 50° para a direita ou esquerda e desloca-a uma unidade em frente |
| colisao-sardinhas | verifica se existe colisão entre sardinhas, matando a sardinha com uma dada probabilidade, se existir |
| colisao-tubaroes | verifica se existe colisão entre tubarões, matando o tubarão com uma dada probabilidade, se existir |
| reproduzir-sardinhas | cria uma nova sardinha com uma dada probabilidade |
| apanhar-sardinhas | permite que os tubarões apanhem sardinhas e se reproduzam |
| morte | mata os tubarões de "causas naturais" com uma dada probabilidade |
| do-plot | actualiza o gráfico de populações |
Código
Variáveis globais
Neste módulo, as variáveis utilizadas são as seguinte:
globals [ geracao ] breeds [ sardinhas tubaroes ] sardinhas-own [ apanhada? ]
Mais uma vez, a variável global GERACAO tem um carácter temporal. A declaração seguinte define a existência de dois tipos de "turtles": as sardinhas e os tubarões. Existe ainda uma variável - APANHADA? - que é específica das sardinhas.
Funções principais
Vejamos as funções. Neste módulo temos: preparar, executar, movimento, colisao-sardinhas, colisao-tubaroes, reproduzir-sardinhas, apanhar-sardinhas, morte e do-plot.
preparar
to preparar
ca
set geracao 0
ask patches [ set pcolor blue ]
set-default-shape sardinhas "sardinha"
create-custom-sardinhas numero-inicial-sardinhas
[ set color gray
set size 1.0
setxy random-float screen-size-x random-float screen-size-y
set apanhada? false ]
set-default-shape tubaroes "tubarao"
create-custom-tubaroes numero-inicial-tubaroes
[ set color black
set size 2.0
setxy random-float screen-size-x random-float screen-size-y ]
do-plot
end
A função preparar cria o ambiente gráfico e inicializa o gráfico. Dado que este módulo pretende estudar o comportamento de duas espécies marinhas é conveniente pintar os "patches" de azul, a cor do mar.
ask patches [ set pcolor blue ]
As espécies intervenientes são sardinhas e tubarões. O formato gráfico das "turtles" obtém-se com o comando set-default-shape. Usando create-custom-<espécie> são criadas na janela gráfica o número de "turtles" da espécie correspondente seleccionado pelo utilizador na interface. A cor, o tamanho e as coordenadas são também definidos para as duas espécies. Em relação às sardinhas, à variável APANHADA? toma o valor falso. Mais à frente será analisada a importância desta variável. O comando do-plot inicializa o gráfico a partir das condições iniciais.
executar
to executar
ask sardinhas
[ movimento
if competicao?
[ colisao-sardinhas ]
reproduzir-sardinhas ]
ask tubaroes
[ movimento
if competicao?
[ colisao-tubaroes ]
apanhar-sardinhas
morte ]
do-plot
set geracao geracao + 1
if (not any? tubaroes) or (not any? sardinhas)
[ stop ]
end
A função executar pode ser dividida em quatro blocos: dois deles dizem respeito a cada uma das espécies; o seguinte diz respeito à parte gráfica (do-plot) e à incrementação da variável GERACAO; por último temos um conjunto de instruções que mandam a simulação parar no caso da extinção de uma das espécies.
Os dois blocos referentes às duas espécies são bastante semelhantes (tal como os dois blocos na função preparar). Ambos chamam a função movimento (que faz movimentar as "turtles") e no caso de haver competição chamam as funções respectivas (colisao-sardinhas e colisao-tubaroes) que produzem os efeitos de competição em função do valor dos parâmetros COMPETICAO-SARDINHAS e COMPETICAO-TUBAROES, especificado na interface.
Funções auxiliares
movimento
to movimento rt random-float 50 - random-float 50 forward 1 end
Esta função movimento é característica destes módulos de dinâmica de populações. A primeira linha faz com que a "turtle" mude a sua direcção de um ângulo aleatório (com uma amplitude angular de 100 graus centrada na direcção do movimento). A segunda linha desloca-as em frente.
colisao-sardinhas
As duas funções seguintes têm uma estrutura igual, sendo uma aplicada às sardinhas e a outra aos tubarões.
to colisao-sardinhas if (any? other-sardinhas-here) and (random-float 100 < competicao-sardinhas) [ die ] end
colisao-tubaroes
to colisao-tubaroes if (any? other-tubaroes-here) and (random-float 100 < competicao-tubaroes) [ die ] end
Basicamente as duas funções verificam se há sobreposição de duas turtles da mesma espécie no mesmo patch e em caso afirmativo resultam na morte de uma das turtles em função do parâmetro de competição dado para cada espécie.
reproduzir-sardinhas
to reproduzir-sardinhas
if random-float 100 < reproducao-sardinhas
[ hatch 1
[ rt random-float 360
forward 1 ] ]
end
A função reproduzir-sardinhas, como o nome indica, faz com que as sardinhas se reproduzam, em função do parâmetro REPRODUCAO-SARDINHAS, escolhido na interface. Mais uma vez, o número de "turtles" que nascem em cada iterada é dado de uma forma estatística. O comando hatch faz aparecer uma nova "turtle". Os seguintes (rt e forward) colocam-na num patch ao lado do pai.
apanhar-sardinhas
to apanhar-sardinhas
locals [ presa ]
without-interruption
[ set presa random-one-of sardinhas-here with [ not apanhada? ]
if presa != nobody
[ set apanhada?-of presa true ] ]
if presa != nobody
[ ifelse random-float 100 < predacao-sardinhas
[ ask presa
[ die ] ]
[ set apanhada?-of presa false ]
if random-float 100 < reproducao-tubaroes
[ hatch 1
[ rt random-float 360
forward 1 ] ] ]
end
Esta função é a mais complexa de todas, não aparecendo nenhuma semelhante noutro módulo. Como tal, merece uma explicação mais detalhada.
Primeiro define-se uma variável local - PRESA - que estará associada a uma "turtle" que se encontre no mesmo patch que um tubarão (não esquecer que esta função é executada dentro da função executar pelos tubarões). De seguida dentro de um without-interruption (as outras turtles são postas em espera até terminarem todas as instruções) é seleccionada uma sardinha que se encontre no mesmo "patch" que um tubarão.
set presa random-one-of sardinhas-here with [ not apanhada? ]
Dado que a função é chamada pelos tubarões, quando a simulação procura uma sardinha (random-one-of sardinhas-here) procura-a no mesmo patch onde se encontra o tubarão. A variável APANHADA? é inicializada na função preparar com o valor false logo à partida todas as sardinhas estarão nestas condições (not apanhada?). Resumindo, associa-se presa a uma sardinha que se encontre no mesmo patch que um tubarão (se existirem sardinhas nestas condições), tomando a sua variável APANHADA? o valor true. Este procedimento, de marcar as sardinhas, serve para evitar que a mesma sardinha seja comida por dois tubarões diferentes.
Uma vez seleccionadas as presas, passamos então à predação. Se existir uma presa (if presa != nobody) então a sua predação e consequente morte serão dadas pelo parâmetro PREDACAO-SARDINHAS de uma forma estatística. Com o comando ifelse são dadas duas hipóteses: Se o número gerado aleatoriamente for menor que o parâmetro então a presa morre; caso contrário, a presa sobrevive, e a sua variável APANHADA? volta a tomar o valor false.
Esta função trata ainda da reprodução dos tubarões dada também de uma forma estatística em função do parâmetro REPRODUCAO-TUBAROES.
morte
to morte if random-float 100 < mortalidade-tubaroes [ die ] end
A função morte equilibra a dinâmica da população dos tubarões. Em relação às sardinhas a sua dinâmica é regida por dois factores que se opõem: reprodução e predação. Considera-se, pois, que as causas de morte natural são dominadas pelas pelos efeitos de predação. Quanto aos tubarões, não existem efeitos que contrabalancem a sua reprodução a não ser morte natural. Este efeito é reproduzido por esta função, cuja estrutura é semelhante a outras já descritas.
do-plot
Por último, a função que trata da componente gráfica: do-plot.
to do-plot set-current-plot "Populacoes" set-current-plot-pen "sardinhas" plot count sardinhas set-current-plot-pen "tubaroes" plot count tubaroes end
Os comandos são bastante simples. A primeira linha selecciona o gráfico a realizar (Populações), sendo este gráfico constituído por duas curvas: sardinhas e tubarões. O comando set-current-plot-pen selecciona a curva correspondente e a linha seguinte traduz a variável reproduzida na curva (no primeiro caso sardinhas e no segundo tubarões).
Início
Variantes e Extensões
Procure introduzir efeitos de mortalidade por causas naturais na população das sardinhas, para além dos causados pela predação
Nos gráficos realizados tem-se as POPULACOES em função da GERACAO. Procure fazer um outro gráfico da forma tubarões vs sardinhas.
Início
©opyright 2004, Centro de Física Teórica e Computacional Programa baseado no programa Wolf Sheep Predation desenvolvido por Wilensky, U. & Reisman, K. (1999)